Los logaritmos son una herramienta matemática fundamental que permite transformar multiplicaciones complejas en sumas más sencillas. Su invención se atribuye a John Napier en el siglo XVII, y han sido cruciales para simplificar cálculos en diversas disciplinas, desde la astronomía hasta la economía. En esencia, un logaritmo responde a la pregunta: ¿a qué exponente debe elevarse una base específica para obtener un número dado? Esto formula la relación entre la base, el logaritmo y el resultado de la operación exponencial.
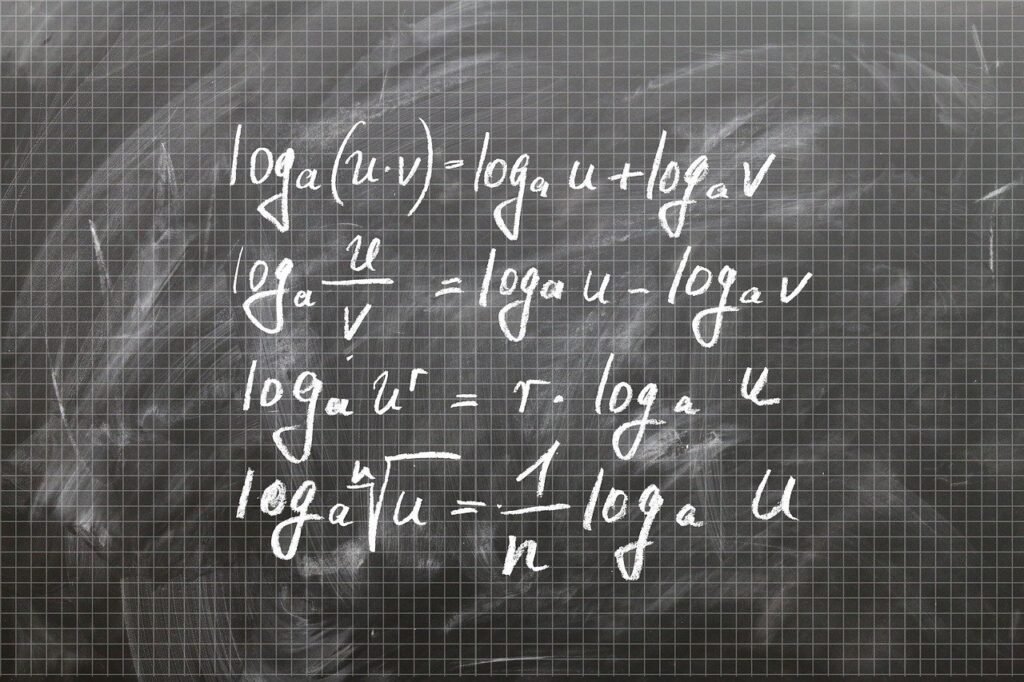
El simbolismo de los logaritmos es bastante sencillo. Por ejemplo, en la notación logb(x) = y, ‘b’ representa la base del logaritmo, ‘x’ es el número cuyo logaritmo se busca y ‘y’ es el exponente al que hay que elevar ‘b’ para obtener ‘x’. Las bases más comunes son 10 (logaritmo decimal) y ‘e’ (logaritmo natural), así como la base 2, que se utiliza con frecuencia en matemáticas avanzadas y ciencias de la computación. Cada tipo de logaritmo tiene su propia utilidad en el contexto de las ecuaciones y el cálculo, lo que subraya la importancia de entenderlos en profundidad.
La comprensión de los logaritmos es especialmente relevante en el contexto del cálculo y la resolución de ecuaciones diferenciales. Los logaritmos no solo simplifican operaciones aritméticas complejas, sino que también facilitan la resolución de problemas que involucran crecimientos exponenciales, como poblaciones, finanzas y ciencia de datos. Al aprender sobre los logaritmos, se adquiere una habilidad esencial que apoya no solo el desarrollo matemático, sino también la aplicación práctica en diversas áreas del conocimiento.
Definición matemática de logaritmo

El logaritmo es una operación matemática que inversamente se relaciona con la exponenciación. En términos sencillos, el logaritmo de un número indica cuántas veces debemos multiplicar un número base para obtener dicho número. Matemáticamente, se puede expresar como: si b es la base y x es el resultado, entonces el logaritmo de x en base b se denota como logb(x) y se define a partir de la relación by = x, donde y es el logaritmo de x en base b.
Por ejemplo, consideremos el logaritmo en base 10 (también conocido como logaritmo decimal). Si tomamos el número 1000, podemos determinar que log10(1000) = 3, ya que 10 multiplicado por sí mismo tres veces es igual a 1000 (10 x 10 x 10 = 1000). De manera similar, para un logaritmo en base 2, si tenemos 8, podemos escribir log2(8) = 3, dado que 2 elevado a la tercera potencia resulta en 8 (2 x 2 x 2 = 8).
El logaritmo puede ser de cualquier base, aunque las más comunes son bases como 10 (logaritmo decimal) y e (logaritmo natural). Esta operación matemática es muy útil en diversas áreas, incluyendo matemáticas puras, ingeniería y ciencias económicas, ya que permite simplificar cálculos complejos y resolver ecuaciones exponenciales. Además, los logaritmos ofrecen herramientas para el análisis de datos, sobre todo en situaciones donde se presentan progressiones o crecimientos exponenciales, lo cual es frecuente en el mundo actual.
Propiedades de los logaritmos
Los logaritmos poseen varias propiedades fundamentales que son esenciales para simplificar y resolver problemas matemáticos, especialmente en el marco de la aritmética. Estas propiedades incluyen la ley del producto, la ley del cociente y la ley de la potencia, las cuales merecen ser examinadas detenidamente.
La ley del producto establece que el logaritmo de un producto de números es igual a la suma de sus logaritmos individuales. Matemáticamente, esto se expresa como: log_b(M * N) = log_b(M) + log_b(N). Por ejemplo, si deseamos calcular log_10(100) + log_10(10), gracias a la ley del producto, esto puede simplificarse a log_10(1000), lo que resulta en 3, puesto que 1000 es igual a 10 elevado a la potencia 3.
La ley del cociente, por otro lado, permite el cálculo del logaritmo de un cociente dividiendo el logaritmo del numerador por el logaritmo del denominador. Se formula como: log_b(M/N) = log_b(M) – log_b(N). Por ejemplo, al calcular log_2(32) – log_2(8), utilizamos la ley del cociente para llegar a log_2(4), que es igual a 2, dado que 4 es 2 elevado a la segunda potencia.
Por último, la ley de la potencia es crucial cuando se trabaja con exponentes. Indica que el logaritmo de una potencia es igual al exponente multiplicado por el logaritmo de la base. Esta ley se expresa como: log_b(M^p) = p * log_b(M). Por ejemplo, log_10(1000) puede ser calculado como 3 * log_10(10), resultando nuevamente en 3.
En resumen, estas tres propiedades de los logaritmos, al ser aplicadas, no solo simplifican los cálculos aritméticos, sino que también proporcionan una comprensión más profunda de cómo los logaritmos interactúan con los números y las operaciones matemáticas básicas.
Tipología de logaritmos: logaritmos en base 10 y base e
Los logaritmos son fundamentales en diversas áreas de la matemática y sus aplicaciones se extienden a la ciencia y la ingeniería. Dos de las bases más comunes de logaritmos son el logaritmo decimal, que utiliza la base 10, y el logaritmo natural, que emplea la base e, donde e es un número irracional aproximadamente igual a 2.71828. Estas bases son particularmente relevantes por sus aplicaciones y propiedades específicas que facilitan el cálculo.
El logaritmo en base 10, también conocido como logaritmo decimal, se indica comúnmente como log(x). Este tipo de logaritmo es útil para estimar y resolver problemas en situaciones cotidianas, como el cálculo de pH en química o la escala Richter para medir terremotos. Al ser una base comúnmente utilizada, facilita la comprensión de varios procesos exponenciales en ámbitos prácticos y académicos.
Por otro lado, el logaritmo natural es denotado como ln(x) y es crucial en el cálculo y la teoría de números. La base e se presenta en múltiples contextos, como el crecimiento exponencial y la teoría de probabilidades. El logaritmo natural aparece a menudo en ecuaciones diferenciales y es fundamental en procesos de modelado matemático, así como en la estadística y la economía, donde describe fenómenos como el interés compuesto y el crecimiento de poblaciones.
A pesar de sus diferencias, ambos tipos de logaritmos son intercambiables mediante un cambio de base, lo que implica que la comprensión de uno puede ayudar en la comprensión del otro. Además, la habilidad para trabajar con diferentes logaritmos es esencial para resolver aplicaciones logarítmicas en matemáticas avanzadas, haciendo de ellos herramientas valiosas para los profesionales en diversos campos del conocimiento.
Logaritmos en la resolución de ecuaciones
Los logaritmos son herramientas fundamentales en la resolución de ecuaciones exponenciales debido a su capacidad para transformar las variables de la ecuación. En esencia, los logaritmos permiten convertir multiplicaciones en sumas y potencias en productos, lo que facilita el proceso de resolución. Cuando se tiene una ecuación de la forma a^x = b, donde a es la base, x es el exponente, y b es el resultado, se puede aplicar logaritmos para despejar la variable x.
Para ilustrar este proceso, consideremos el siguiente ejemplo: supongamos que tenemos la ecuación 2^x = 16. Para resolverla utilizando logaritmos, primero se observa que 16 puede ser expresado como una potencia de 2, específicamente 2^4. De esta manera, podemos reformular la ecuación a^x = b en logaritmos, tomando logaritmos en ambos lados. Aplicando logaritmo, la ecuación sería log(2^x) = log(16). Utilizando la propiedad de los logaritmos que establece que log(a^b) = b * log(a), podemos escribir x * log(2) = log(16).
A continuación, resolvemos por x, dividiendo ambos lados por log(2), lo que nos da x = log(16) / log(2). Al calcular estos logaritmos, obtenemos x = 4, confirmando que 2^4 efectivamente iguala a 16. Este procedimiento no solo ilustra cómo se transforman las ecuaciones mediante logaritmos, sino que también resalta su utilidad en la resolución de problemas donde las exponentes son incógnitas.
Otro ejemplo común es resolver una ecuación como 3^x = 9. Primero, se reconoce que 9 también puede expresarse como una potencia de 3, es decir, 3^2. Aplicando el mismo enfoque, llegamos a la ecuación x = log(9) / log(3), que nos dará x = 2 tras las calculaciones apropiadas. Este método demuestra la efectividad de los logaritmos para simplificar y resolver ecuaciones exponenciales de diversas formas.
Relación entre logaritmos y aritmética
La relación entre logaritmos y aritmética es fundamental en el desarrollo de las matemáticas, ya que los logaritmos proporcionan una herramienta poderosa para simplificar cálculos complejos. En esencia, un logaritmo responde a la pregunta: ¿a qué potencia debe elevarse un número base para obtener un determinado valor? Este concepto permite transformar multiplicaciones y divisiones en sumas y restas, lo que facilita enormemente los cálculos matemáticos. Por ejemplo, la multiplicación de dos números, como a y b, puede expresarse mediante logaritmos como log(a * b) = log(a) + log(b). De esta manera, operacion se convierte en una simple suma, lo que ahorra tiempo y reduce errores en cálculos manuales.
Históricamente, la utilización de logaritmos en aritmética tuvo un impacto significativo antes de la llegada de las calculadoras, especialmente a través de la creación de tablas de logaritmos. Estas tablas permitían a los matemáticos y científicos, así como a ingenieros, realizar cálculos complejos más eficientemente. Por ejemplo, en el siglo XVII, los logaritmos fueron popularizados por John Napier y, más tarde, por otros matemáticos como Henry Briggs, quienes fueron pioneros en el desarrollo de estas tablas. Gracias a estas contribuciones, se podían realizar cálculos que, de otro modo, habrían requerido un tiempo y esfuerzo considerable.
Además, la conexión entre logaritmos y aritmética se extiende a diversas áreas de la ciencia y la ingeniería, donde se requieren cálculos precisos. La propiedad de los logaritmos para transformar multiplicaciones en adiciones permite a los científicos diseñar experimentos y realizar mediciones con mayor eficacia. Por estas razones, los logaritmos siguen siendo una parte integral del arsenal aritmético en la educación matemática actual.
Aplicaciones prácticas de los logaritmos
Los logaritmos tienen una amplia gama de aplicaciones prácticas que van más allá de la teoría matemática. En ciencias, por ejemplo, los logaritmos son fundamentales para la química, donde se utilizan en el cálculo del pH, que se define como el logaritmo negativo de la concentración de iones hidrógeno en una solución. Este enfoque permite a los científicos cuantificar la acidez o alcalinidad de una solución de manera efectiva y comprensible, facilitando el trabajo en laboratorios y aplicaciones industriales.
En ingeniería, el uso de logaritmos se extiende al análisis de circuitos eléctricos, donde la relación entre corriente y voltaje se puede expresar a través de funciones logarítmicas. Este tipo de análisis ayuda a los ingenieros a diseñar y optimizar sistemas que dependen de la electricidad, asegurando así una mayor eficiencia y seguridad en sus proyectos. El uso de logaritmos en el modelo de crecimiento exponencial también es crucial en la ingeniería de sistemas, particularmente en el tratamiento de señales y control de sistemas.
La economía también se beneficia del uso de logaritmos, especialmente en el análisis de datos económicos y la modelación de crecimiento. Por ejemplo, las tasas de crecimiento económico se suelen expresar en términos logarítmicos para facilitar su comparación a lo largo del tiempo. Los logaritmos ayudan a descomponer tasas compuestas en tasas simples, lo que permite que economistas y analistas interpreten mejor los datos financieros y realicen proyecciones más precisas.
Finalmente, en el campo de la tecnología, los logaritmos son esenciales en la informática, especialmente en algoritmos de búsqueda y en la teoría de la información. Por ejemplo, el logaritmo en base 2 se utiliza para medir la complejidad de algoritmos, además de servir como base para entender la compresión de datos y la criptografía, integral para la seguridad en el mundo digital actual. Estas diversas aplicaciones enfatizan la importancia de los logaritmos como una herramienta clave en la modelización y resolución de problemas en diversas disciplinas.
Ejercicios prácticos sobre logaritmos
Para fortalecer el conocimiento adquirido sobre los logaritmos, es fundamental realizar ejercicios prácticos que permitan a los lectores aplicar los conceptos aprendidos. A continuación, se presentan una variedad de problemas con sus respectivas soluciones que facilitarán la comprensión de este tema matemático clave.
Ejercicio 1: Calcula el logaritmo base 10 de 1000.
Solución: Para resolver esto, utilizamos la definición de logaritmo: log10(x) = y significa que 10y = x. En este caso, buscamos log10(1000). Observamos que 1000 puede expresarse como 103, por lo que log10(1000) = 3.
Ejercicio 2: Encuentra el valor de log2(16).
Solución: Aplicamos la propiedad de los logaritmos. Reconocemos que 16 es 24, por lo tanto log2(16) = 4 porque 24 = 16.
Ejercicio 3: Resuelve la ecuación logb(x) = 3 para x y un valor de b = 5.
Solución: Al sustituir b en nuestra ecuación, se obtiene log5(x) = 3. Esto implica que 53 = x, por lo cual x = 125.
Estos ejercicios salvaguardan no solo la práctica, sino que también iluminan la relación entre los logaritmos y las operaciones aritméticas comunes. A medida que se resuelven, es importante tener en cuenta las propiedades de los logaritmos, como el logaritmo del producto, el cociente y las potencias, que enriquecen el aprendizaje. Para lograr dominar los logaritmos, se recomienda seguir practicando con problemas variados que fortalezcan la intuición detrás de estos conceptos.
Conclusión
En resumen, los logaritmos constituyen una herramienta fundamental en el campo de las matemáticas, proporcionando un método eficiente para resolver ecuaciones exponentiales y simplificando cálculos complejos. A lo largo del artículo, hemos examinado cómo los logaritmos se definen como la operación inversa de la exponenciación, permitiendo transformar relaciones multiplicativas en sumas. Este concepto no solo es crucial en la aritmética, sino que también se extiende a otros ámbitos como la estadística, la teoría de números y diversas ciencias aplicadas.
Además, es importante reconocer que el uso de logaritmos resulta esencial para el análisis de datos, ya que permite manejar grandes números de manera más efectiva y facilita la comprensión de tendencias de crecimiento en diferentes disciplinas. Por ejemplo, en la biología, los logaritmos son útiles para describir poblaciones que crecen exponencialmente. Asimismo, en la economía, se utilizan para modelar fenómenos de crecimiento y cálculo de tasas de interés compuestas. Esta versatilidad resalta la relevancia de los logaritmos en múltiples contextos.
Finalmente, para aquellos interesados en profundizar en el tema, se sugiere dedicar tiempo a la práctica de logaritmos y sus propiedades. A través de ejercicios y aplicaciones prácticas, se puede alcanzar un grado de dominio que no solo mejora la comprensión matemática, sino que también brinda habilidades esenciales para el análisis crítico en situaciones del mundo real. La exploración continua de los logaritmos permitirá a los estudiantes y profesionales en diversas áreas beneficiarse de esta poderosa arena del conocimiento matemático.
¿Quieres referenciar en formato APA este artículo?
Castañeda, S. (28 de octubre de 2025). ¿Qué es un Logaritmo y Cómo se Relaciona con la Aritmética?. Paraíso Académico. Recuperado de: https://paraisoacademico.com/que-es-un-logaritmo-y-como-se-relaciona-con-la-aritmetica/
