Definición de Ángulo Completo
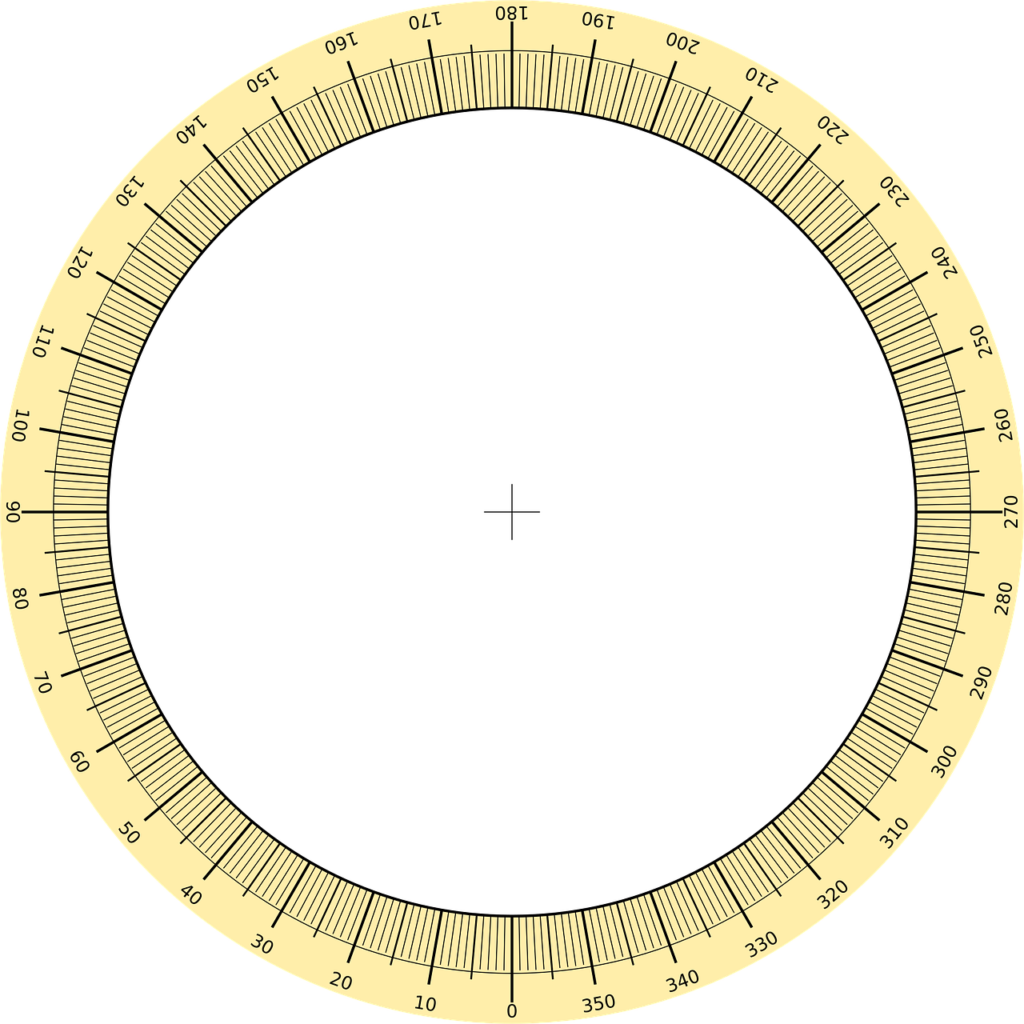
Un ángulo completo se define como aquel que abarca exactamente 360 grados. Esta medida representa un giro completo en el plano, regresando al mismo punto de inicio. La noción de ángulo completo es fundamental dentro de la geometría, ya que establece la base para entender otras formas de medir ángulos, como los ángulos rectos, obtusos y agudos. En arquitecturas, diseños e incluso en la navegación, el concepto de un ángulo completo juega un papel crucial al determinar trayectorias y ángulos de incidencia.
Es importante señalar que los ángulos completos pueden ser considerados no solo en términos de grados. También es posible expresarlos en radianes, donde un ángulo completo corresponde a 2π radianes. Esta dualidad en la representación permite a matemáticos y científicos trabajar de manera eficaz en diversas aplicaciones. Por ejemplo, en el campo de la trigonometría, la comprensión de los ángulos completos es vital para resolver problemas que involucran circularidades, ya que se utilizan patrones cíclicos y funciones periódicas.
Para ilustrar este concepto, consideremos un reloj. Cuando las manecillas del reloj completan un ciclo completo desde las 12 hasta las 12 nuevamente, esto representa un ángulo completo de 360 grados. Este ejemplo visual contribuye a facilitar la comprensión del ángulo completo en un contexto cotidiano. A medida que se avanza en el estudio de la geometría y el análisis de los ángulos, la posición de estos en un círculo unitario también se convierte en un aspecto significativo, donde el ángulo completo no solo tiene aplicaciones prácticas, sino que también proporciona un entendimiento profundo de las relaciones angulares en una variedad de disciplinas matemáticas. La relación entre los ángulos en diferentes contextos resalta la importancia de dominar la definición de un ángulo completo.
Características del Ángulo Completo
El ángulo completo es una figura geométrica fundamental en el estudio de la geometría y la trigonometría. Se define como aquella que resulta de una rotación que cubre un recorrido total de 360 grados o 2π radianes en un plano. Esta característica lo distingue de otros ángulos, como el ángulo recto, que mide 90 grados, y el ángulo agudo, que posee una medida menor a 90 grados. El ángulo completo, al abarcar una rotación total, se representa gráficamente como una línea recta que regresa a su punto de inicio, formando un perímetro cerrado.
En términos de su representación gráfica, el ángulo completo se puede visualizar como un círculo completo, donde el vértice se ubica en el centro del círculo y los lados del ángulo se extienden hasta tocar la circunferencia del mismo. Esta visualización resulta útil para entender la naturaleza cíclica del ángulo completo y su relación con el movimiento circular. Por otro lado, el ángulo completo es importante en la utilización de fórmulas trigonométricas, donde se observa que su seno es igual a cero y su coseno es igual a uno en el sistema de coordenadas cartesianas.
Asimismo, el ángulo completo se encuentra presente en diversos contextos prácticos. En la ingeniería y la arquitectura, se utiliza para describir rotaciones completas de estructuras alrededor de un eje. En el ámbito de la física, se relaciona con fenómenos periódicos, como la oscilación de un péndulo. La versatilidad del ángulo completo se manifiesta a través de su capacidad para ser parte de cálculos más complejos, como el determinante de áreas y volúmenes en los cuales se opera con figuras tridimensionales.
Ejemplos Prácticos del Ángulo Completo
El ángulo completo, que se define como un giro de 360 grados, se encuentra presente en una variedad de contextos en la vida cotidiana y en diversas disciplinas. Uno de los ejemplos más evidentes es en la arquitectura, donde los edificios y estructuras a menudo se diseñan con elementos que giran en un ciclo completo. Por ejemplo, las columnas circulares o los arcos que rodean muchas plazas públicas juegan con la idea del ángulo completo, creando un entorno armonioso y estéticamente agradable.
En el diseño gráfico, el ángulo completo también es fundamental. Los diseñadores utilizan el concepto para crear logotipos, iconos y otras composiciones visuales que requieren una simetría perfecta. Un logo circular que enfatiza la continuidad y la integridad puede ser un excelente ejemplo del uso del ángulo completo en el diseño. De este modo, la comprensión de los ángulos se convierte en una herramienta clave para lograr un diseño efectivo y atractivo.
Adicionalmente, en la ingeniería, especialmente en el ámbito de la mecánica, el ángulo completo se aplica en el diseño de maquinaria rotativa. Considerando, por ejemplo, un engranaje que completa una rotación completa, se observa cómo el ángulo completo permite que la máquina funcione de manera eficiente y efectiva en diversas aplicaciones. Las relaciones de movimiento y cómo las partes interactúan son fundamentales y están intrínsecamente ligadas al uso de los ángulos completos.
Para ilustrar aún más el concepto, propongo un ejercicio práctico. Imagina que te encuentras atornillando una tapa circular en su lugar. Al hacerlo, puedes visualizar perfectamente cómo el ángulo completo hace que la tapa encaje a la perfección. Intenta calcular el área de un círculo utilizando el radio y recuerda que cualquier movimiento dentro de ese círculo puede estar directamente relacionado con el ángulo completo. Esta integración del concepto en situaciones cotidianas impulsa el aprendizaje activo y permite apreciar su relevancia en nuestro entorno.
Importancia del Ángulo Completo en Matemáticas y Ciencias
El ángulo completo, definido como la medida que abarca 360 grados, es un concepto fundamental en diversas ramas de las matemáticas y ciencias. Su relevancia se extiende no solo a la geometría, donde se utiliza para describir la forma y el espacio, sino también a la trigonometría, que se ocupa de las relaciones entre los ángulos y lados de los triángulos. En trigonometría, el conocimiento del ángulo completo permite a los estudiantes comprender mejor conceptos como la periodicidad de las funciones trigonométricas. Estas funciones representan la relación entre el ángulo y las proporciones de los lados de un triángulo rectángulo, herramientas esenciales en el análisis de situaciones reales.
Asimismo, en física, el ángulo completo es crucial para describir el movimiento circular y la dinámica de los cuerpos en rotación. Por ejemplo, cuando se estudia la cinemática de un objeto que gira, comprender cómo se relacionan los ángulos completos con el tiempo y la velocidad angular resulta fundamental para resolver problemas. Además, el concepto de ángulo completo permite modelar fenómenos como la oscilación, lo cual es indispensable en campos como la ingeniería y la arquitectura, donde se aplican principios físicos en la práctica.
La adquisición de un entendimiento sólido del ángulo completo proporciona una base sobre la cual se pueden desarrollar temas más avanzados en matemáticas y ciencias. A medida que los estudiantes avanzan en sus estudios, los conceptos relacionados con el ángulo completo interfieren en diversas ámbitos, facilitando la resolución de problemas complejos y el desarrollo de aplicaciones prácticas. Por lo tanto, el papel del ángulo completo no debe ser subestimado, ya que es fundamental para formar la estructura del conocimiento en tráficos académicos y profesionales.
¿Quieres referenciar en formato APA este artículo?
Castañeda, S. (05 de diciembre de 2025). Ángulo completo. Paraíso Académico. Recuperado de: https://paraisoacademico.com/angulo-completo/
